Companion for OLS Chapter
This page has been moved to https://econ.pages.code.wm.edu/407/notes/docs/index.html and is no longer being maintained here.
This companion to the OLS Chapter shows how to implement the models in both Stata and R. Unless stated otherwise, the code shown here is for R. Note, we use a panel dataset (multiple time periods per individual) and arbitrarily restrict our analysis to a cross section dataset by analyzing only records where time is 4. We do this for demonstration purposes only- it is usually a horrible idea to throw away data like this, and later in the course we will learn more about panel data techniques.
# allows us to open stata datasets
library(foreign)
# for heteroskedasticity corrected variance/covariance matrices
library(sandwich)
# for White Heteroskedasticity Test
library(lmtest)
# for bootstrapping
library(boot)
# for column percentiles
library(matrixStats)
tk.df = read.dta("https://rlhick.people.wm.edu/econ407/data/tobias_koop.dta")
tk4.df = subset(tk.df, time == 4)
histwage <- hist(tk4.df$ln_wage,main = "Log Wage",xlab="ln_wage")
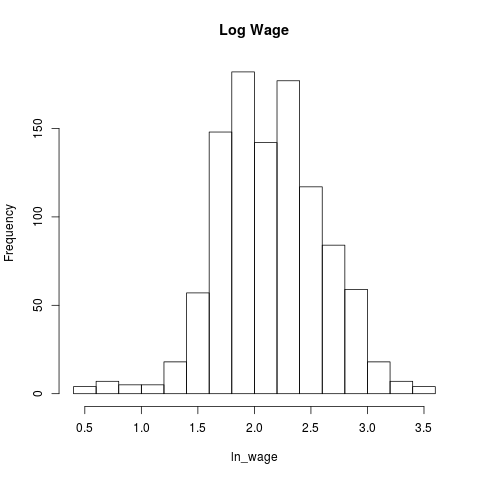
The OLS Model
Using ln_wage as our dependent variable, here is the code for running a simple OLS model in stata and R. First in Stata. Since we haven't loaded the data yet, let's do that and run the model:
webuse set "https://rlhick.people.wm.edu/econ407/data/"
webuse tobias_koop
keep if time==4
regress ln_wage educ pexp pexp2 broken_home
set more off
(prefix now "https://rlhick.people.wm.edu/econ407/data")
(16,885 observations deleted)
Source | SS df MS Number of obs = 1,034
-------------+---------------------------------- F(4, 1029) = 51.36
Model | 37.3778146 4 9.34445366 Prob > F = 0.0000
Residual | 187.21445 1,029 .181938241 R-squared = 0.1664
-------------+---------------------------------- Adj R-squared = 0.1632
Total | 224.592265 1,033 .217417488 Root MSE = .42654
------------------------------------------------------------------------------
ln_wage | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
educ | .0852725 .0092897 9.18 0.000 .0670437 .1035014
pexp | .2035214 .0235859 8.63 0.000 .1572395 .2498033
pexp2 | -.0124126 .0022825 -5.44 0.000 -.0168916 -.0079336
broken_home | -.0087254 .0357107 -0.24 0.807 -.0787995 .0613488
_cons | .4603326 .137294 3.35 0.001 .1909243 .7297408
------------------------------------------------------------------------------
In R, we use
ols.lm = lm(ln_wage~educ + pexp + pexp2 + broken_home, data=tk4.df)
summary(ols.lm)
Call:
lm(formula = ln_wage ~ educ + pexp + pexp2 + broken_home, data = tk4.df)
Residuals:
Min 1Q Median 3Q Max
-1.69490 -0.24818 -0.00079 0.25417 1.51139
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.460333 0.137294 3.353 0.000829 ***
educ 0.085273 0.009290 9.179 < 2e-16 ***
pexp 0.203521 0.023586 8.629 < 2e-16 ***
pexp2 -0.012413 0.002283 -5.438 6.73e-08 ***
broken_home -0.008725 0.035711 -0.244 0.807020
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4265 on 1029 degrees of freedom
Multiple R-squared: 0.1664, Adjusted R-squared: 0.1632
F-statistic: 51.36 on 4 and 1029 DF, p-value: < 2.2e-16
Robust Standard Errors
Note that since the \(\mathbf{b}\)'s are unbiased estimators for \(\beta\), those continue to be the ones to report. However, our variance covariance matrix is \[ VARCOV_{HC1} = \mathbf{(x'x)^{-1}V(x'x)^{-1}} \]
Defining \(\mathbf{e=y-xb}\), \[ \mathbf{V} = diag(\mathbf{ee}') \]
In stata, the robust option is a very easy way to implement the robust standard error correction. Note: this is not robust regression.
regress ln_wage educ pexp pexp2 broken_home, robust
Linear regression Number of obs = 1,034
F(4, 1029) = 64.82
Prob > F = 0.0000
R-squared = 0.1664
Root MSE = .42654
------------------------------------------------------------------------------
| Robust
ln_wage | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
educ | .0852725 .0099294 8.59 0.000 .0657882 .1047568
pexp | .2035214 .0226835 8.97 0.000 .1590101 .2480326
pexp2 | -.0124126 .0022447 -5.53 0.000 -.0168173 -.0080079
broken_home | -.0087254 .0312381 -0.28 0.780 -.070023 .0525723
_cons | .4603326 .1315416 3.50 0.000 .2022121 .718453
------------------------------------------------------------------------------
Implementing this in R, we can use the sandwich package's `vcovHC` function with the `HC1` option (stata default):
VARCOV = vcovHC(ols.lm, 'HC1')
se = sqrt(diag(VARCOV))
print(se)
(Intercept) educ pexp pexp2 broken_home 0.131541623 0.009929445 0.022683530 0.002244678 0.031238081
Note that the F-statistic reported by the R OLS result above is inappropriate in the presence of heteroskedasticity. We need to use a different form of the F test. Stata does this automatically. In R, we need to use waldtest for the correct model F statistic:
waldtest(ols.lm, vcov = vcovHC(ols.lm,'HC1'))
Wald test Model 1: ln_wage ~ educ + pexp + pexp2 + broken_home Model 2: ln_wage ~ 1 Res.Df Df F Pr(>F) 1 1029 2 1033 -4 64.82 < 2.2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
So far, we have gotten R to provide us with the correct robust standard error regression results but it isn't in a single table. To put it together for printing, use
# copy summary object
robust.summ = summary(ols.lm)
# overwrite all coefficients with robust counterparts
robust.summ$coefficients = unclass(coeftest(ols.lm, vcov. = VARCOV))
# overwrite f stat with correct robust value
f_robust = waldtest(ols.lm, vcov = VARCOV)
robust.summ$fstatistic[1] = f_robust$F[2]
print(robust.summ)
Call:
lm(formula = ln_wage ~ educ + pexp + pexp2 + broken_home, data = tk4.df)
Residuals:
Min 1Q Median 3Q Max
-1.69490 -0.24818 -0.00079 0.25417 1.51139
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.460333 0.131542 3.500 0.000486 ***
educ 0.085273 0.009929 8.588 < 2e-16 ***
pexp 0.203521 0.022684 8.972 < 2e-16 ***
pexp2 -0.012413 0.002245 -5.530 4.06e-08 ***
broken_home -0.008725 0.031238 -0.279 0.780057
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4265 on 1029 degrees of freedom
Multiple R-squared: 0.1664, Adjusted R-squared: 0.1632
F-statistic: 64.82 on 4 and 1029 DF, p-value: < 2.2e-16
The bootstrapping approach to robust standard errors
Given the advent of very fast computation even with laptop computers, we can use boostrapping to correct our standard errrors for any non-iid error process. In R, we run this (and by asking for percentiles) to get non-parametric bootstrap estimates for confidence intervals:
bs_ols <- function(formula, data, indices) {
d <- data[indices,] # allows boot to select sample
fit <- lm(formula, data=d) # runs the model for this sample
return(coef(fit)) # returns coefficients
}
results <- boot(data=tk4.df, statistic=bs_ols,
R=1000, formula=ln_wage~educ + pexp + pexp2 + broken_home)
From that we can extract the 95\% confidence intervals from the 1000 replicates.
ci_mat = colQuantiles(results$t,probs=c(.025,.975))
ci = data.frame(ci_mat,row.names=c("Intercept","educ","pexp","pexp2","broken_home"))
colnames(ci) = c("2.5%","97.5%")
print(ci)
2.5% 97.5%
Intercept 0.19939776 0.714556678
educ 0.06565962 0.104340132
pexp 0.16128174 0.249996019
pexp2 -0.01696095 -0.008148125
broken_home -0.07249099 0.056744122
In Stata, we just run (for 1000 replicates) using the following code. I believe this is doing what is called a parametric bootstrap (confidence intervals assume normality). As you can see, the Stata method is much easier to implement.
regress ln_wage educ pexp pexp2 broken_home, vce(bootstrap,rep(1000))
(running regress on estimation sample)
Bootstrap replications (1000)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
.................................................. 150
.................................................. 200
.................................................. 250
.................................................. 300
.................................................. 350
.................................................. 400
.................................................. 450
.................................................. 500
.................................................. 550
.................................................. 600
.................................................. 650
.................................................. 700
.................................................. 750
.................................................. 800
.................................................. 850
.................................................. 900
.................................................. 950
.................................................. 1000
Linear regression Number of obs = 1,034
Replications = 1,000
Wald chi2(4) = 252.66
Prob > chi2 = 0.0000
R-squared = 0.1664
Adj R-squared = 0.1632
Root MSE = 0.4265
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
ln_wage | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
educ | .0852725 .0100503 8.48 0.000 .0655743 .1049707
pexp | .2035214 .022688 8.97 0.000 .1590538 .247989
pexp2 | -.0124126 .0022409 -5.54 0.000 -.0168047 -.0080205
broken_home | -.0087254 .0320888 -0.27 0.786 -.0716183 .0541676
_cons | .4603326 .1340845 3.43 0.001 .1975318 .7231333
------------------------------------------------------------------------------
Testing for Heteroskedasticity
The two dominant heteroskedasticity tests are the White test and the Cook-Weisberg (both Breusch Pagan tests). The White test is particularly useful if you believe the error variances have a potentially non-linear relationship with model covariates. For stata, we need to make sure the basic OLS regression (rather than robust) is run just prior to these commands and then we can use:
quietly regress ln_wage educ pexp pexp2 broken_home
imtest, white
White's test for Ho: homoskedasticity
against Ha: unrestricted heteroskedasticity
chi2(12) = 29.20
Prob > chi2 = 0.0037
Cameron & Trivedi's decomposition of IM-test
---------------------------------------------------
Source | chi2 df p
---------------------+-----------------------------
Heteroskedasticity | 29.20 12 0.0037
Skewness | 14.14 4 0.0068
Kurtosis | 16.19 1 0.0001
---------------------+-----------------------------
Total | 59.53 17 0.0000
---------------------------------------------------
In R, we perform the White test by:
bptest(ols.lm,ln_wage ~ educ*pexp + educ*pexp2 + educ*broken_home + pexp*pexp2 + pexp*broken_home +
pexp2*broken_home + I(educ^2) + I(pexp^2) + I(pexp2^2) + I(broken_home^2),data=tk4.df)
studentized Breusch-Pagan test data: ols.lm BP = 29.196, df = 12, p-value = 0.003685
Notice that in R, we need to specify the form of the heteroskedasticity. To mirror the White test, we include interaction and second order terms. Both Stata's imtest and R's bptest allow you to specify more esoteric forms of heteroskedasticity, although in R it is more apparent since we have to specify the form of the heteroskedasticity for the test to run.
A more basic test- one assuming that heteroskedastity is a linear function of the \(\mathbf{x}\)'s- is the Cook-Weisberg Breusch Pagan test.
In stata, we use
hettest
Breusch-Pagan / Cook-Weisberg test for heteroskedasticity
Ho: Constant variance
Variables: fitted values of ln_wage
chi2(1) = 19.57
Prob > chi2 = 0.0000
R doesn't implement this test directly. But it can be performed manually following these steps:
- Recover residuals as above, denote as \(\mathbf{e}\)
- square the residuals by the sqare root of mean squared residuals:
\[ \mathbf{r} = \frac{diagonal(\mathbf{ee}')}{\sqrt{\mathbf{e'e}/N}} \]
- Run the regression \(\mathbf{r} = \gamma_0 + \gamma_1 \mathbf{xb} + \mathbf{v}\). Recall that \(\mathbf{xb} = \mathbf{\hat{y}}\).
- Recover ESS defined as
\[ ESS = (\mathbf{\hat{r}} - \bar{r})'(\hat{\mathbf{r}} - \bar{r}) \]
- ESS/2 is the test statistic distributed \(\chi^2_{(1)}\)
r = diag(tcrossprod(ols.lm$residuals))/mean(diag(tcrossprod(ols.lm$residuals)))
xb = ols.lm$fitted.values
het_ols_results = lm(r~xb)
mss = crossprod(het_ols_results$fitted.values - mean(r))
cw = mss/2
sprintf("BP / Cook-Weisberg score for heterosk.: %2.3f distributed chi2 with %d df.",cw,1)
[1] "BP / Cook-Weisberg score for heterosk.: 19.572 distributed chi2 with 1 df."